作者: songtianyi create@2022-06-29
在整个去中心化生态里里,P2P(Peer-to-Peer) 都是非常重要且必要的技术,它的特点是,每个节点是等价的,既可以作为 client, 又可以作为 server. 在 C/S 的架构中,client 要连接 server 需要知道 server 的地址,P2P 网络中的节点之间也不例外,我们可以在每个节点中保存所有其它节点的地址信息,并访问。但问题是,如果网络中的节点数量非常庞大,达到百万级别,这样的方式对于内存和存储的消耗就非常大了。本文要讲的内容,Chord 和 Kdemia 算法,就是来解决这个问题的,即,解决节点间如何高效地找到彼此的问题。
我在 《编程核心概念》 中的数据结构和算法小节中有强调过,数据结构作为解决问题的第一关,其实比算法要更重要。对于这个问题,也不例外。我们首先要做的事情是,将离散的节点变的有规律一些,且不改变它的特质。 如下图,这些节点的组织方式不便于我们思考。
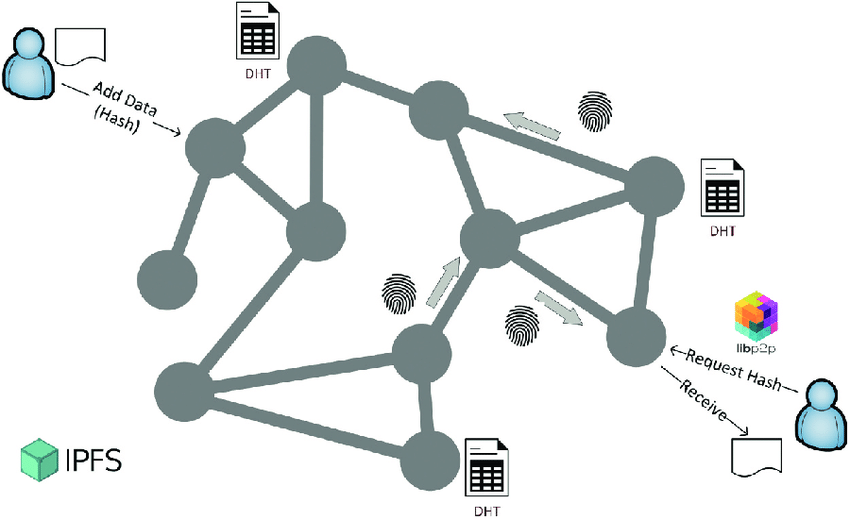
我们可以尝试把它抽象成一个环状的结构, 如下:

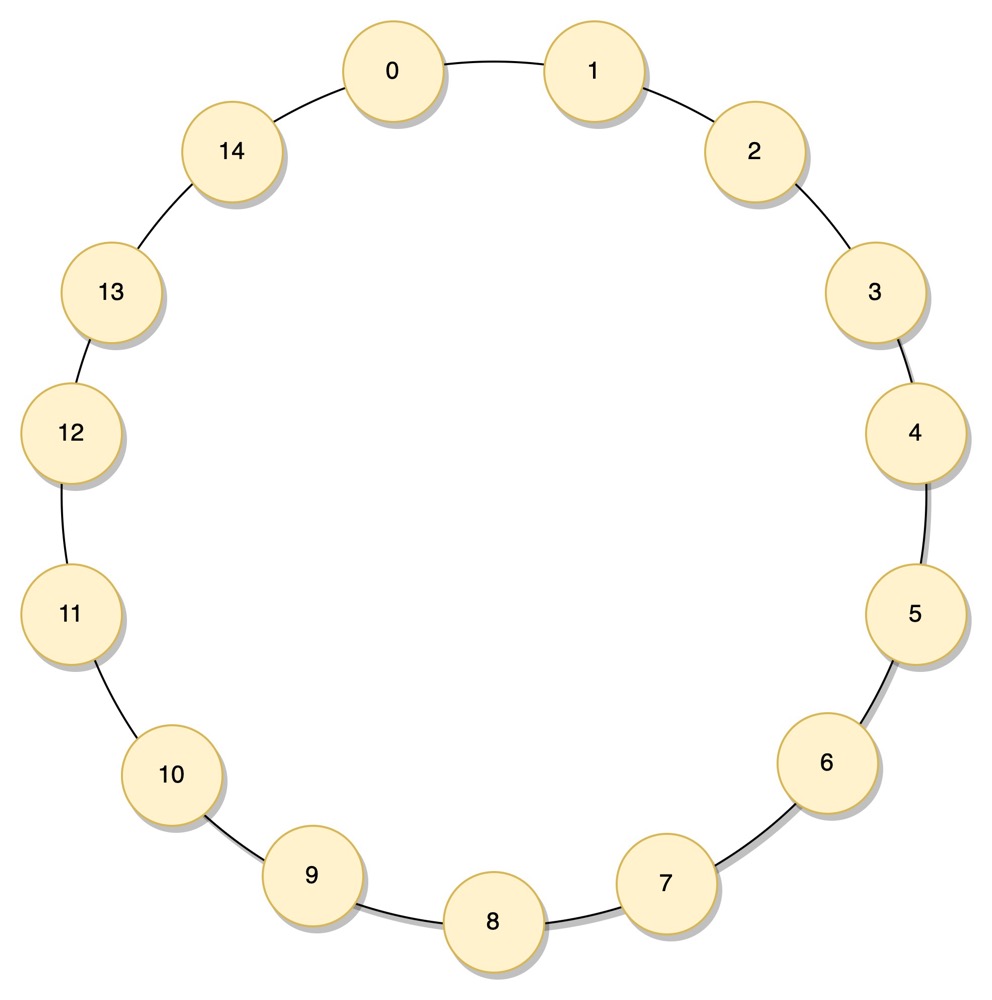
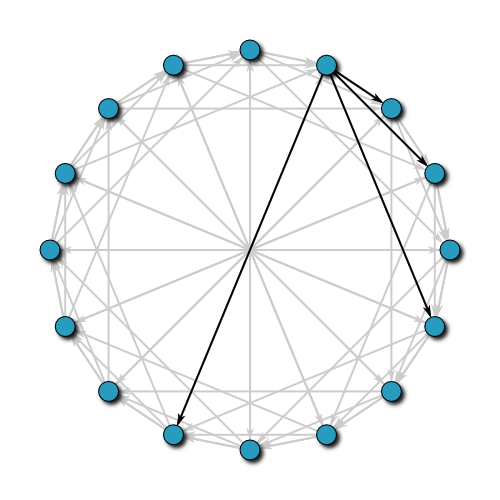
这个环状结构和这些节点的实际网络拓扑并不是对应的,它们之间的真实物理距离也并非像图中所示那样等分的。 如果每个节点保存其相邻节点(如下图所示),我们能很快找到附近的节点,但当节点数比较庞大的时候,并不高效,复杂度为 O(N)
那如果跳着查呢?节点 0 保存了节点 8 的信息,这样节点 8 周围的节点也能较快被找到。
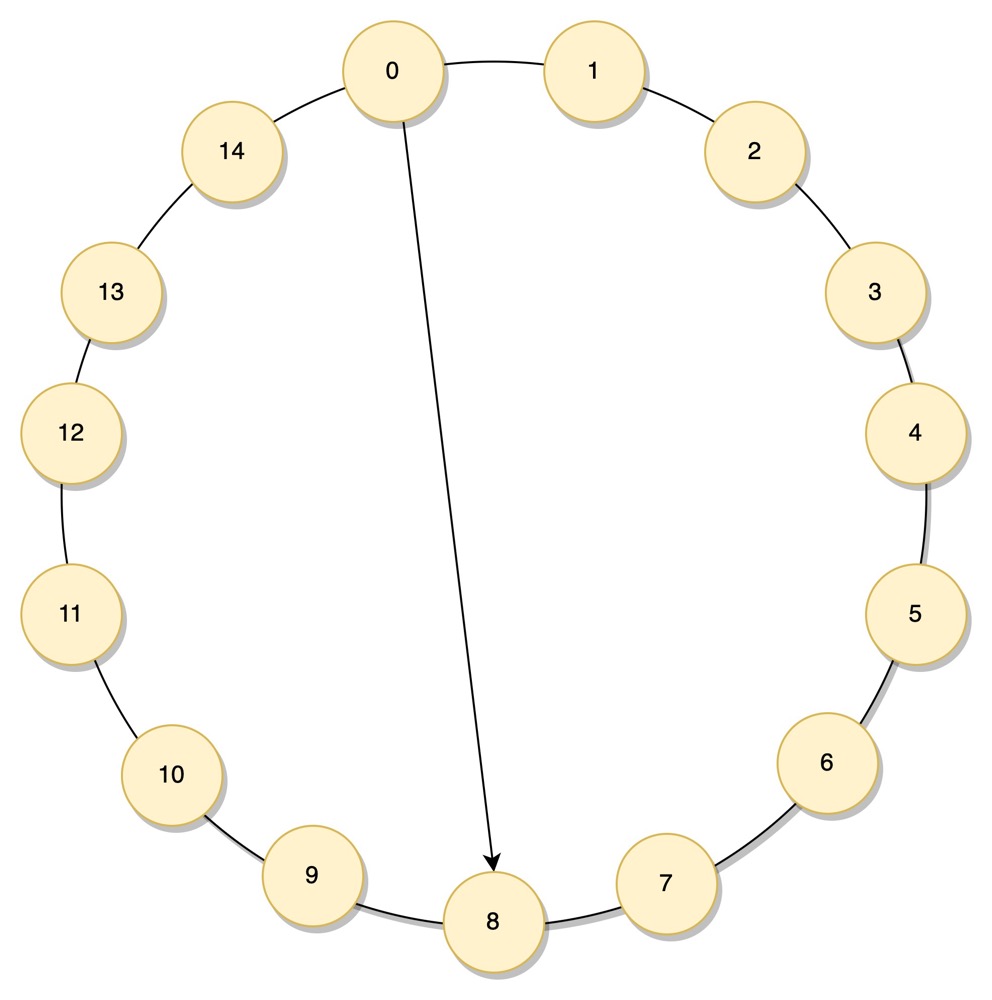
在 《算法优化之时空交换》 一文中有强调,算法优化的思路就是用空间和时间相互转换,找到一个平衡点。在上图中,我们多保存了一个节点的信息,查找效率可以认为提升了1倍,变为 O(N/2), 那么保存越多的节点信息,查找效率越高,但在本文开头,我们也强调了,不可能保存所有的信息(保存所有节点信息的查找复杂度为 O(1)).
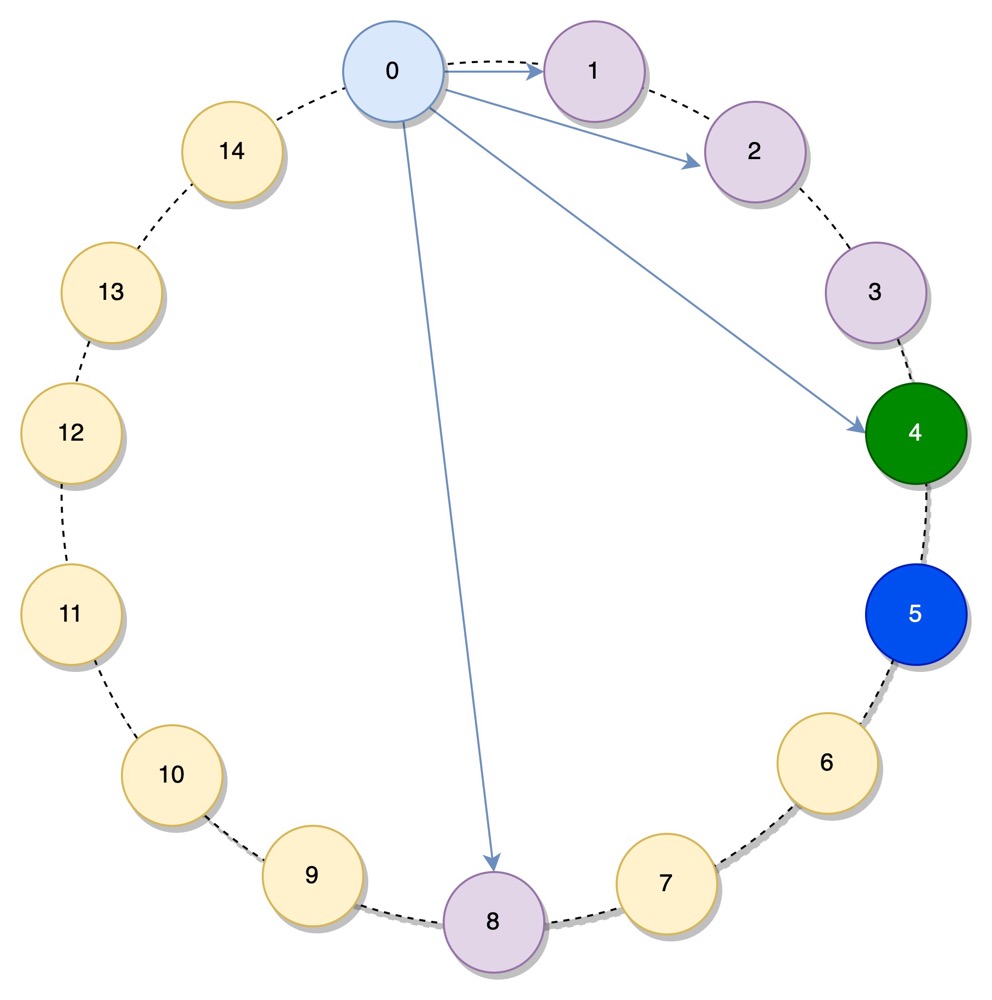
Chord 算法的做法是,每个节点保存最多 m = Ceil(log2N) 个节点的信息,N 为节点数。假设当前节点为 0, 它所保存的节点为 1, 2, 4, 8. 如下图所示:
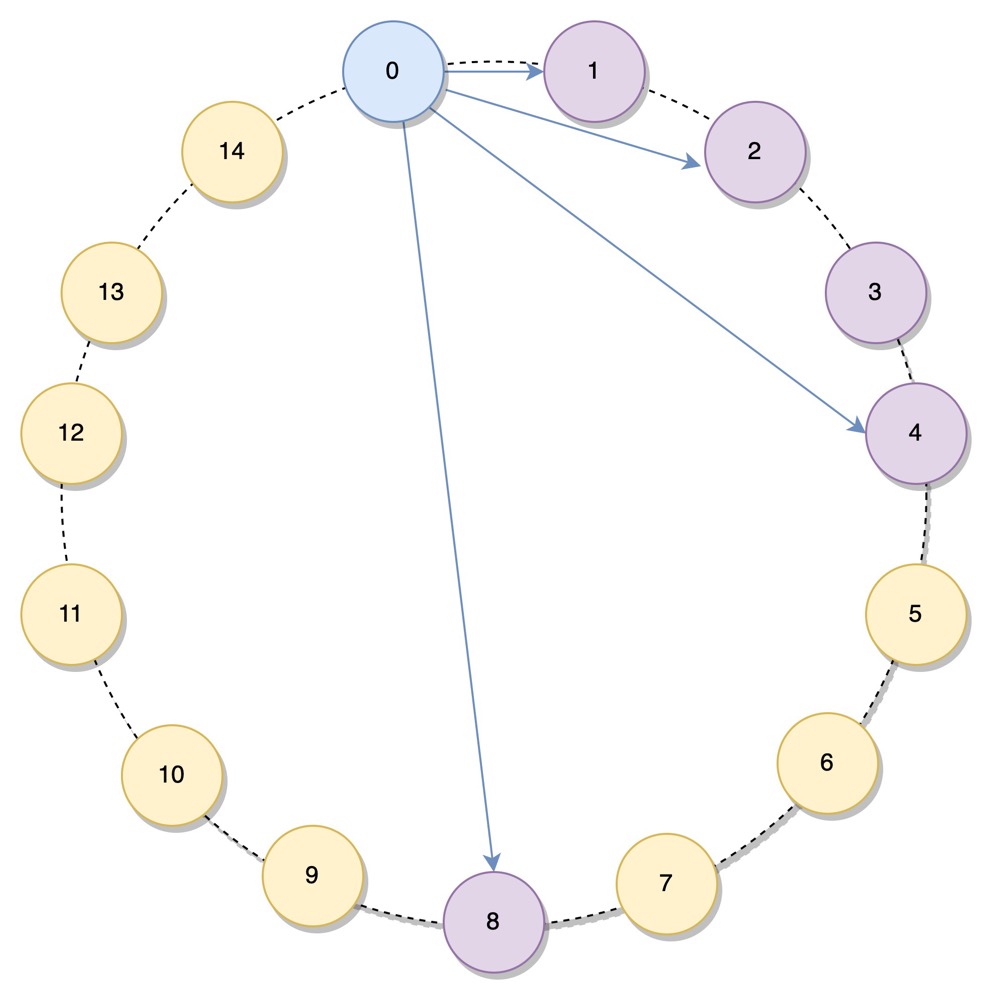
保存节点信息的结构称为 finger table*
节点 1 是 finger table 中顺时针方向的第 1 个值,被称为节点 0 的 successor, 节点 8 是 finger table 中逆时针方向的第 1 个值,被称为节点 0 的 predecessor, 这两个概念会在后面用到
设当前节点为 n, 其 finger table 中第 i (m >= i >= 1) 个值的计算方式为 (n + 2i-1) mod 2m
以 N 为 16 为例,按照上述方法构造出来的图应该如下,其中一个节点的连接情况用粗线标记出来了:
Chord 算法的查找复杂度为 log2N).
查找的伪代码如下:
// ask node n to find the successor of id
n.find_successor(id)
// Yes, that should be a closing square bracket to match the opening parenthesis.
// It is a half closed interval.
if id ∈ (n, successor] then
return successor
else
// forward the query around the circle
n0 := closest_preceding_node(id)
return n0.find_successor(id)
// search the local table for the highest predecessor of id
n.closest_preceding_node(id)
for i = m downto 1 do
if (finger[i] ∈ (n, id)) then
return finger[i]
return n
可以以 n = 0, id = 5 为例,代入跟踪一遍逻辑来体会。
| 节点的增删不在本文讨论范围内 |
Kademlia 的做法和 Chord 的区别主要是节点间的距离计算方式不同。Chord 你可以认为节点 x, y 的 距离计算方式为 𝑑(𝑥, 𝑦) = (𝑥 - 𝑦) mod 2m, 而 Kademlia 的计算公式为 𝑑(𝑥, 𝑦)= height_of_tree - leading_zero_count(𝑥 ^ 𝑦). Chord 是将节点的 ID 映射到一个环上,而 Kademlia 是将节点的 ID 映射到一个二叉树上,如下图:
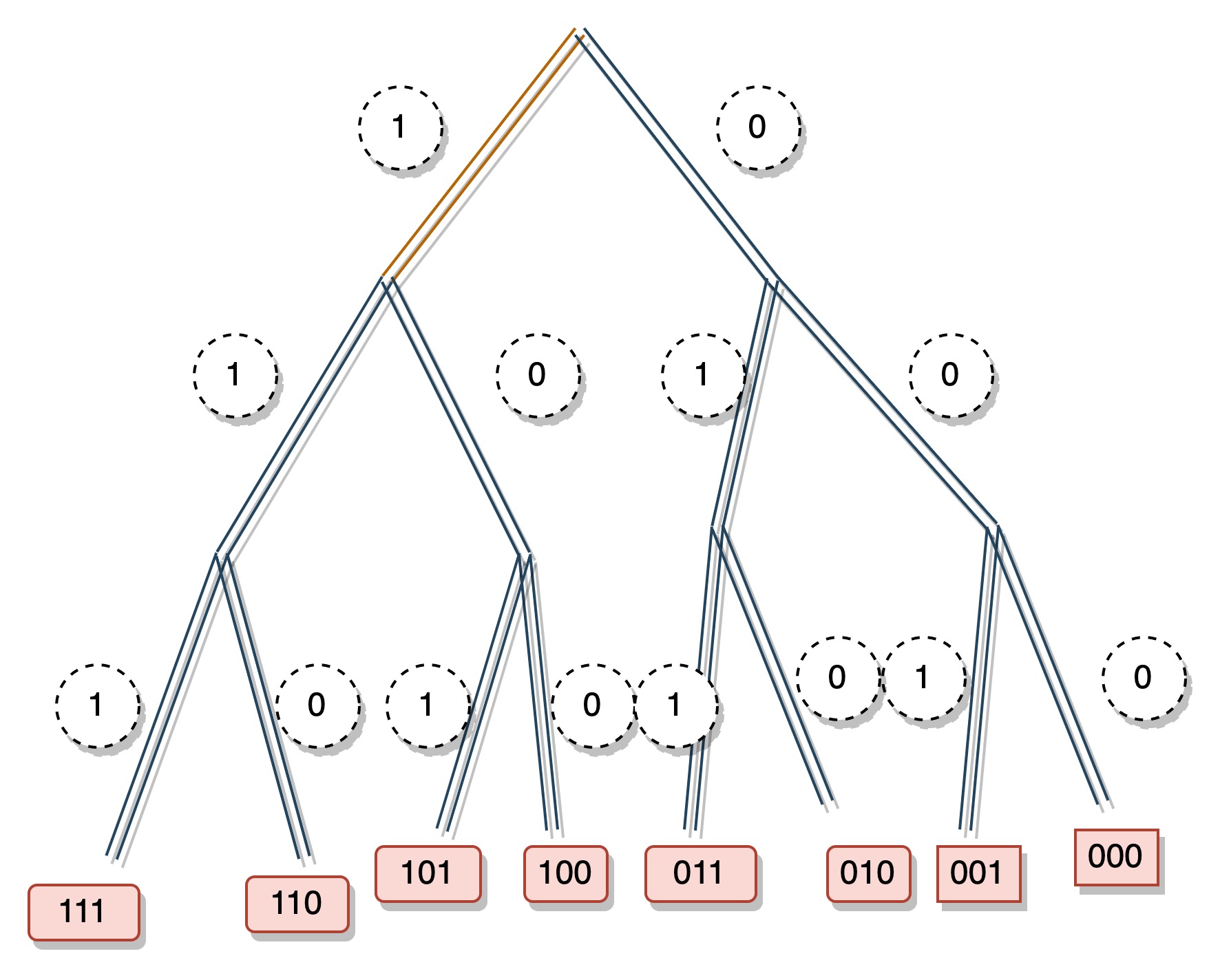
节点 0 和节点 1 的距离为 1,节点 0 和节点 7 的距离为 3
| 0 ^ 7 = 7, 但距离并不是 7, 而是看最长公共前缀的最低高度,0 和 7 没有公共前缀,所以距离是 3. 有些中文博客没有搞清楚这个问题,直接将异或的结果代入计算了,所以看着有些迷糊 |
在 Kademlia 里,用于存储节点信息的结构称为 k-bucket, 和 Chord 中的 finger table 类似。k-bucket 的意思是,将节点按照不同的距离,分别存在不同的 bucket 里,最多有 H 个 bucket, H 为树的高度, 每个 bucket 是一个 list, 长度最大为 k, 且 list 是按照最近使用时间从小到大排序的(sorted by time last seen - least-recently seen node at the head, most recently seen at the tail).
| k 的取值不是固定的,一般为 20, 根据实际场景调整, 感兴趣可以看下论文中的英文解释 |
根据上图,我们以节点 0 为例,它的 bucket 有 3 个,分别用不同颜色标记了出来,如下图所示。
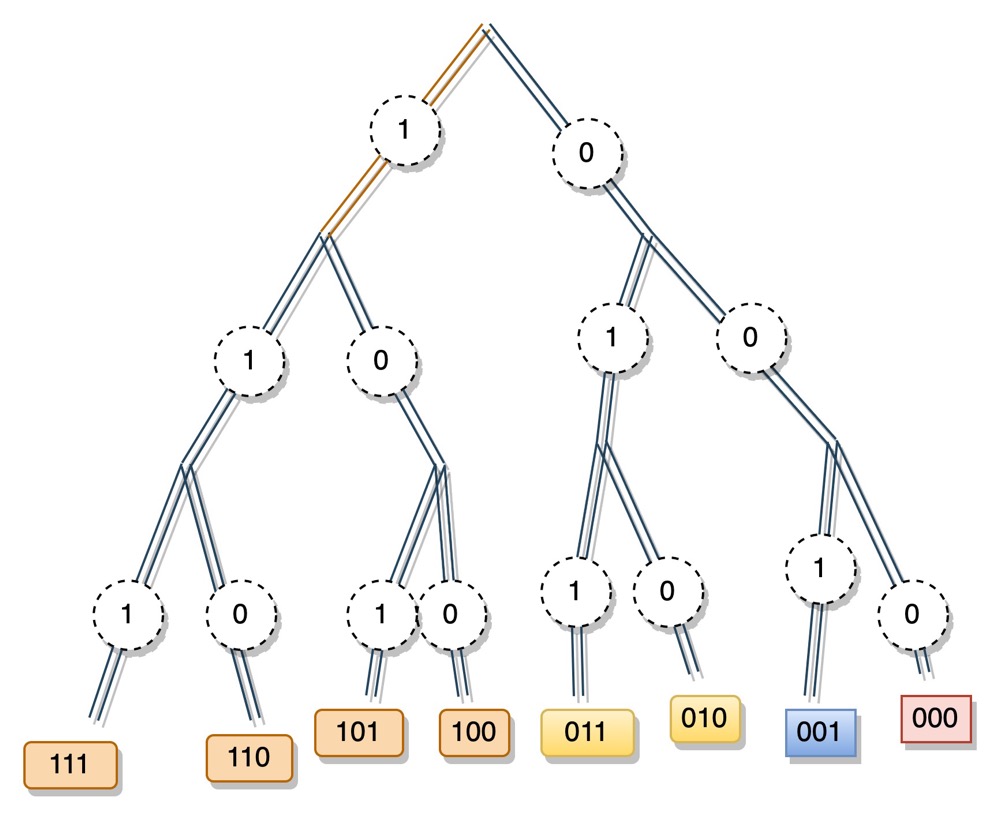
k-bucket 的存储结果如下图所示:

当我们向节点 0 询问节点 7 的信息时,先计算 d(0, 7) = 3, 得知,节点 7 离 bucket[3] 中的节点更近,于是去 bucket[3] 的节点中去找,如果找不到继续迭代即可,这样就可以跳过一部分查找,每次可以跳过一半的数据,这样效率在 log2N.
不管是 Chord 还是 Kademlia, 其实现都要比本文所述的要复杂的多,完整的 P2P 网络的实现需要考虑的因素也会更多。本文主要是说明它们的算法思想