基于 Trie 的防火墙策略搜索方法

前言

在网络工程师对防火墙策略作运维变更时，通常需要知道防火墙是否存在一条或者多条策略满足了当前需求，或者当前需求冲突；需要知道某个端口是否已经被开放等等，因此基于用户输入的五元组信息搜索出关联策略是一个高频需求。暴力的方法是遍历已有策略，根据输入条件进行过滤得到结果，但在金融企业里，当结果可能存在于任意一台防火墙上时，策略总数可能多达十几万条，而且策略之间的对比比较复杂，O(N)的复杂度难以应对高频次的搜索需求。一个简单的优化是对输入和输出作映射并缓存，但并不解决根本问题。

Trie

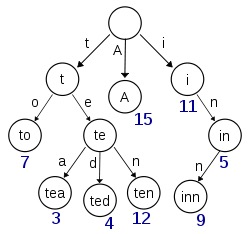
Trie(读作/ˈtriː/)又称前缀树或字典树，是一种有序树，一个节点的所有子孙都有相同的前缀。它的用途很广泛，比如用户搜索提示，当输入一个网址(公共前缀)时，可以从 Trie 中找到所有可能的选择，也可以用于词频统计，字符串查询等方面。

Trie 的构造

对于字符串数组 S, 其元素为:

["A", "to", "tea", "ted", "ten", "i", "in","inn"]

先创建一个空的根节点，枚举 S，对于元素 S_i, 从根节点开始，找到和其第一个字符匹配的节点，如果没有则创建，再以匹配到的节点为始，找到和其第二个字符匹配的节点，如果没有则创建，依次类推，构建出整棵树。最终得到 Trie 结构:

防火墙策略搜索

防火墙策略的搜索是输入的五元组+动作和已有策略的比较过程，如果我们将已有策略划分成不相关的集合(即，有集合 A 和 B，如果策略 P 只存在于 A 或者只存在于 B，那么认为 A 和 B 是不相关的)，并且集合內的策略是有序的，那么比较次数会大大减少。Trie 的树形结构能够表达集合之间的不相交特性，所以适合用 Trie 来表达已有策略，最终搜索已有策略的过程变成搜索 Trie 的过程。

防火墙策略预处理

防火墙策略的结构本质是五元组+动作的六元组，即(SrcAddr, DstAddr, Protocol, SrcPort, DstPort, Action)。

对于地址，我们可以将其转换为数字范围, 比如对于 IP 地址192.168.1.8可以转换成[3232235784, 3232235784, 对于 CIDR 地址址192.168.1.0/25, 它的可用范围为192.168.1.1~192.168.1.126, 转换成数字范围为[3232235777, 3232235902]
对于协议，可以将其转换成数字，比如 TCP 可以转成 6
对于端口，部分防火墙使用字符串表示端口，比如 www 代表 80 等等，将其转换成数字形式
如果协议是 ICMP/ICMP6, 它的 type 和 code 也可以用数字表示
对于动作，用 0 表示 deny，用 1 表示 accept
对于 any，可以用-1 表示

经过预处理的策略表示为:

R = (a, p, [sal, sar], [dal, dar], [spl, spr], [dpl, dpr])

构造策略树

现有经过预处理的已有策略数组 S, S = [R₁, R₂, …, R_n], 其 Json 格式为:

{  
   "S":[  
      {  
         "sal":167876354,
         "sar":167876354,
         "dal":3232244222,
         "dar":3232244222,
         "p":6,
         "spl":0,
         "spr":65535,
         "dpl":88,
         "dpr":88,
         "a":1
      },
      {  
         "sal":3232243969,
         "sar":3232243969,
         "dal":3232235777,
         "dar":3232235777,
         "p":6,
         "spl":0,
         "spr":65535,
         "dpl":80,
         "dpr":80,
         "a":1
      },
      {  
         "sal":3232243969,
         "sar":3232243969,
         "dal":3232235809,
         "dar":3232235809,
         "p":6,
         "spl":0,
         "spr":65535,
         "dpl":80,
         "dpr":80,
         "a":1
      },
      {  
         "sal":3232244001,
         "sar":3232244001,
         "dal":3232235789,
         "dar":3232235789,
         "p":6,
         "spl":0,
         "spr":65535,
         "dpl":80,
         "dpr":80,
         "a":1
      },
      {  
         "sal":167903844,
         "sar":167903844,
         "dal":167838052,
         "dar":167838052,
         "p":17,
         "spl":0,
         "spr":65535,
         "dpl":2667,
         "dpr":65535,
         "a":0
      },
      {  
         "sal":3232235886,
         "sar":3232235887,
         "dal":3232235976,
         "dar":3232235976,
         "p":-1,
         "spl":0,
         "spr":65535,
         "dpl":0,
         "dpr":65535,
         "a":1
      },
      {  
         "sal":-1,
         "sar":-1,
         "dal":-1,
         "dar":-1,
         "p":-1,
         "spl":0,
         "spr":65535,
         "dpl":0,
         "dpr":65535,
         "a":1
      }
   ]
}

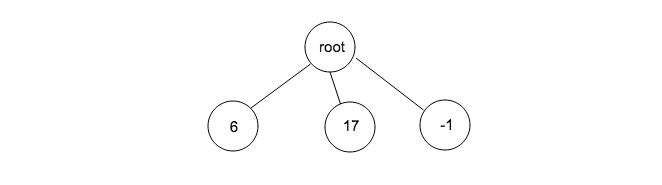
我们可以把一个六元组看成 trie 树例子中的字符串，依次处理六元组的每个元素。比如对于协议，我们的构造的结果如图所示:

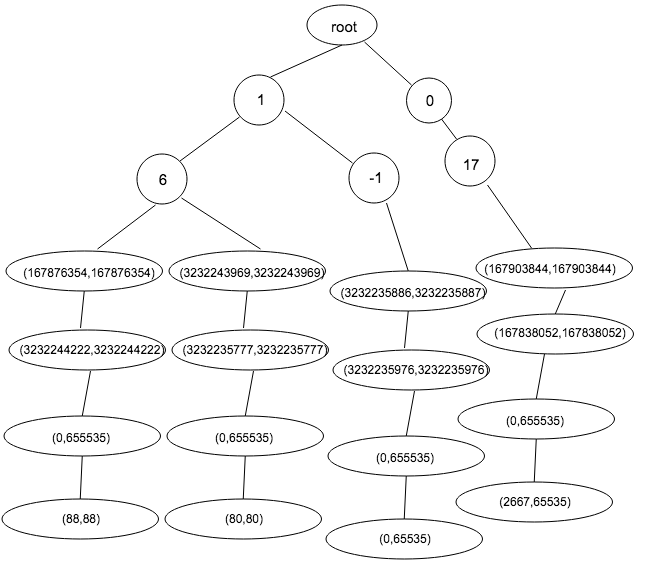
以此类推，构造出整棵树, 由于图片大小限制，只给出部分构造，并且省略了保存策略的叶子结点:

这里以策略(3232243969, 3232243969, 3232235809, 3232235809, 6, 0, 65535, 80, 80, 1)为例, 从策略树中找出包含该策略的策略，流程如下:

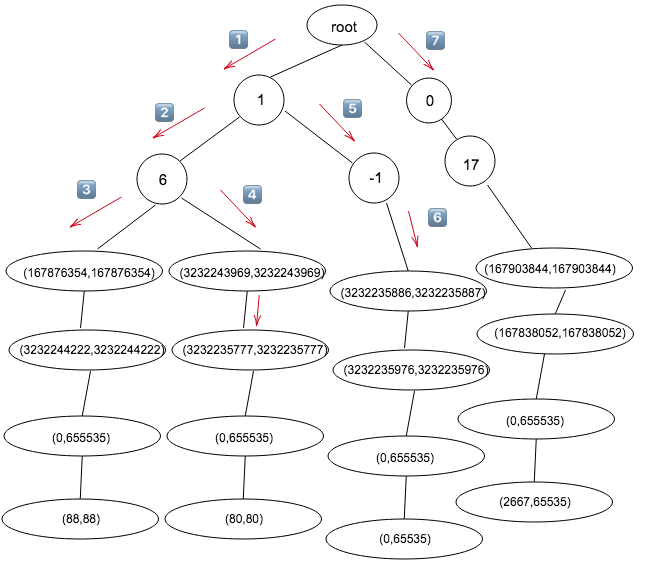
从图中可以看出， 0 所在的分枝被立即排除在结果集之外，达到了优化比较次数的目的，但效果有限。

不相交特性

看了上图你会发现，我们在搜索的时候需要遍历某个节点的所有子节点，比如第二步和第五步，这是因为我们在构造策略树没有保证它们的不相交特性，结果存在于 6 分枝的叶子结点中，也可能存在于 -1 分枝的叶子结点中，因为 -1 是包含 6 的。同样的，五元组的每个元素都存在这个问题，所以只能称之为部分不相交。

参考资料

小白详解 Trie 树