作者: songtianyi 2018-08-14
1 分钟
机器学习的热度一直不减,其相关技术必然是未来程序猿的必修课,要学就趁早。在深度学习领域,python 应该是不二之选,python 作为一门胶水语言,拥有极其丰富的第三方库,不管解决什么问题,它都应该是比较快的工具,值得大家学习。Julia 是一个面向科学计算的高性能动态高级程序设计语言,其语法与其他科学计算语言(Matlab)相似,而且在许多情况下拥有能与编译语言相媲美的性能。值得一提的是,tensorflow 和 mxnet 都有 julia 的 binding,对于新手,可以尝试用 julia 打开机器学习的大门, 作为老手,学习一门新语言,也能打开视野,为未来的技术变迁做储备。在开始之前,请先掌握语言选型里的概念。
Julia is a highly productive language that runs fast
快
性能是 julia 设计的初衷。科学计算需要大量的性能开销,主流的 python 并不能满足这一要求,但 julia 的设计者们仍然认为动态语言是更好的选择,得益于技术的进步,动态语言可以达与静态语言相媲美的性能,于是 julia 在 2012 年诞生了(python 诞生于 1991)
动态类型
optional typing
通常,动态语言的变量类型都是在运行时确定的,但对于 julia 来说是可选的,你可以在代码中申明类型,利用 JIT,julia 可以编译部分代码以提高性能,这些声明为 JIT 提供了用于优化性能的信息。Julia 提供了预编译的选项 __precompile__()。
多重派发(multiple dispatch)
类似于静态语言的函数重载,julia 在处理同名函数时使用的方法叫多重派发。多重派发是 julia 的核心特性。
多范式,IP,PP,OOP,FP,MP
通用性
虽然 Julia 是为科学计算而设计的,但也注重在其他领域的应用,所以在语法设计上不仅参考了 R, MATLAB, Python,也同时吸取了 Lisp, Perl, Lua, Ruby 等语言的优点。
coroutine(Task)
可以直接调用 C,没有额外的封装
支持宏
即时编译(Just-In-Time)技术或者叫即时编译器。我们知道,静态语言是通过编译器将源码编译成机器码来执行的,只需编译一次;动态语言是通过解释器在程序运行时一句句边翻译边运行的,同一段代码可能需要翻译多次。即时编译则是两者的结合,即时编译器在运行时逐句翻译代码并执行,并将翻译结果缓存(具体的逻辑依赖于 JIT 的算法实现),相对于解释器,性能开销要低很多。
在官方Dowload页面下载指定平台的安装包或者二进制包,本文使用的版本为0.6.4, julia 还在快速迭代中,不同版本之间会有差异。安装好之后,可以直接执行,它会启动一个和 python 一样的交互式的 shell(repl):
./julia
也可以用它来执行 julia 代码:
julia demo.jl
在此之前,你可能需要把 julia 二进制加入环境变量中,比如 macOS 下:
JULIA="/Applications/Julia-0.6.app/Contents/Resources/julia/bin/"
export PATH=$PATH:$JULIA
更多的用法请查看它的 help 文档。
| Lang | Typed | Static and dynamic checks | Strongly checked | Weakly or strongly typed | Dynamically or statically typed | Type theories | Paradigms |
|---|---|---|---|---|---|---|---|
| Julia | ☑️ | ❌ | ☑️ | weakly | dynamically | generic, overloading, subtype | IP,SP,PP,OOP,FP,MP |
dynamic checks: Julia 是动态语言,只有动态检查,所谓的编译也是发生在运行时的。
strongly checked: 关于类型系统的安全性检查,一直是一个比较难界定的问题,julia 的 commiter 认为 julia 属于 strongly checked 的语言 [2], 他给出的理由是:
没有指针运算
没有类型双关(type punning)
关于类型双关,简单来说就是通过一些奇技淫巧(通常是用指针操作内存),绕过语言的类型系统,从而达到用该语言语法难以实现甚至不可能达到的效果, 这在 C 语言里是很常见的。一个安全的类型系统当然是不允许这么做的。类型双关的具体定义可以参考 wikipedia[3], 还是比较容易理解的。
在语言选型里讲到过,拥有隐式类型转换的语言属于 weakly checked,我们来看下面的例子:
julia> pi + 1
4.141592653589793
浮点和整形可以相加,julia 进行了隐式类型转换?不是,我们在 repl 里用?加表达式来看看 repl 给我们的解释
help?> pi + 1
+(x, y...)
Addition operator. x+y+z+... calls this function with all arguments, i.e. +(x, y, z, ...).
说明这里只是语法糖, Julia 称之为type promotion。当我们需要类型转换的时候可以使用convert函数。
julia> convert(Float64, pi + 1)
4.141592653589793
weakly typed: 类型是可变的
a = 10
a = "b"
println(a)
dynamically typed: 类型在运行时确定
There is no meaningful concept of a "compile-time type": the only type a value has is its actual type when the program is running.
type inference: julia 支持类型推断。需要注意的地方是,在不同 bit 的硬件架构下,推断出的类型会不同
# 32-bit system:
julia> typeof(1)
Int32
# 64-bit system:
julia> typeof(1)
Int64
nominative: 意味着类型之间的关系是通过名称和显式的类型关系声明来确定的,和通过类型结构来确定类型关系的 structural type system 相对。
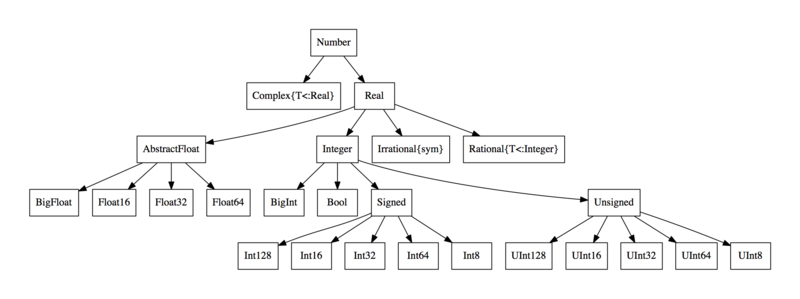
julia 的类型系统定义了一个类型树(type graph),根类型是Any, 是所有类型的 super type,叶子类型是Union{},是所有类型的 subtype,这里只列出数值类型部分:

在这个类型树里 Float64, Int64 等都是 Number 类型的子类,以此为例,我们来看下 julia 的多态的书写形式,很简单:
function print(x ::Number)
println("this is ", x)
end
print(1.0::Float64)
print(4::Int64)
output:
1.0
4
julia 的多态属于 nominal subtyping
julia 的泛型可以应用在复合类型上
julia> struct Point{T}
x::T
y::T
end
我们可以通过实例化一个泛型来创建一个新的类型
Point{String}
它和不使用泛型的形式的效果是一样的:
struct Point
x::String
y::String
end
而且 Point 本身也是一个类型对象(type object),它是所有 Point{T}实例的父类型
julia> Point{Float64} <: Point
true
julia> Point{AbstractString} <: Point
true
tip: A <: B为真则 A 是 B 的子类型成立
但是 julia 泛型的类型规则属于不变(invariant), 意味着,当Float64 <: Real为真时,Point{Float64} <: Point{Real}并不为真,它不会保持或者逆转之前的类型关系。因此,当泛型实例作为入参类型时会面临一个问题, 比如函数入参类型为 Point{Real},这时我们不能对它传入 Point{Float64},验证代码如下:
struct Point{T}
x::T
y::T
end
function norm(p::Point{Real})
return sqrt(p.x^2 + p.y^2)
end
println(norm(Point{Real}(1.0, 1.0)))
println(norm(Point{Float64}(1.0, 1.0))) # MethodError: no method matching norm(::Point{Float64})
解决的方式是,我们用一个类型范围来限定入参类型,而不是一个具体类型:
struct Point{T}
x::T
y::T
end
function norm(p::Point{<:Real}) # 所有使用 Real 子类型实例化的 Point{T}都可以作为入参
return sqrt(p.x^2 + p.y^2)
end
println(norm(Point{Real}(1.0, 1.0)))
println(norm(Point{Float64}(1.0, 1.0))) # OK
泛型也可以应用在抽象类型上:
abstract type Point{T} end
或者基础类型上
primitive type String{T} 32 end
| 类型 | 解释 |
|---|---|
| Int8, UInt8, Int16, UInt16, Int32, UInt32, Int64, UInt64, Int128, UInt128 | 整形 |
| Char, String | 字符/字符串, String 能够使用下标索引, 注意: Julia 的下标都是从 1 开始的, 1-based. 关于 String 的更多内容可以查看strings |
| Bool | 真假值 |
| Float16, Float32, Float64 | IEEE754-2008 浮点, 2.5e-4, 1e10, 0.5f0, 0x1.8p3(16 进制浮点), Inf32, -Inf32, Inf, -Inf, …, NaN, NaN16 |
| Any | 任意类型 |
| 类型 | 解释 |
|---|---|
| Complex | 复数类型, i 用 im 表示 ex. 0 + 4im |
| Rational | 分数 ex. 6//9, 即 9 分之 6 |
| function | 函数,函数的定义在 julia 有更简洁的方法,ex. f(x, y) = x + y, 这种写法更贴合科学计算里的公式。当然,函数名也可以是 Unicode 字符, ∑(x,y) = x + y。在 julia 里,算术运算符属于函数的语法糖。 |
| Tuple | 元组,t = (1, 2,"a") |
| Channel | 管道,先进先出的队列 |
| Abstract | 抽象类型 |
| struct | 结构体 |
| mutable | 修饰类型的是否可修改 |
| Union | 联合类型 |
| Nullable | 当一个值不确定它是否存在时可以使用 Nullable 来封装它,保证访问的安全性,类似于 Java 的 Optional<T> |
| Task | coroutine |
在 Julia 里函数是一等公民(first-class objects), 你能够将函数赋值给变量,也可以作为参数和返回值。
julia> f = x -> x*x + 2*x - 1
(::#13) (generic function with 1 method)
julia> f(2)
7
julia> g = x -> x^2 + 2x - 1
(::#15) (generic function with 1 method)
julia> g(2)
7
函数的返回值可以为元组
julia> f = (x, y) -> (x, y)
(::#25) (generic function with 1 method)
julia> x,y = f(1,2)
(1, 2)
和 python 一样,函数的入参可以带默认值
julia> f = (x, y=1) -> x + y
(::#28) (generic function with 2 methods)
julia> f(2)
3
并且支持隐式 return。
当多个函数的逻辑在概念上(conceptual)相同时,我们倾向于使用相同的名称,比如两个类型的想加,会使用add来命名。那么自然就存在一个问题,如何选择要执行的函数?选择要执行的函数的过程称为派发(dispatch),派发分为三种:
julia 使用 mutiple dispatch。
和泛型不同的是,Tuple 的类型规则是协变(covariant), 意味着,如果有 Int32 <: Number,那么Tuple{Int32} <: Tuple{Number} 为真,
Julia 的 Channel 和 Go 的 chan 在使用上基本是一致的。
创建一个没有 buffer 的 channel, channel 的写入会被阻塞,直到有人读取它。
// go
ch := make(chan int, 0)
// julia
ch = Channel(0)
创建一个带 buffer 的 channel
// go
ch := make(chan int, 10)
// julia
ch = Channel(10)
使用 put!和 take!来写入和读取数据, 和 golang 的区别是,julia 的 channel 在定义时可以不指定类型,默认为Any,意味着可以写入任意类型的数据。
ch = Channel{String}(10)
put!(ch, "Hello")
put!(ch, "World")
take!(ch)
take!(ch)
关闭 channel。julia 的 channel 在关闭后仍然可以读取数据,直到为空。
close(ch)
判断是否有数据
isready(ch)
比 go chan 方便的地方是,Channel 提供了 fetch 函数,fetch 只会读取数据,不会 remove 掉数据
Channel 可以和一个函数相绑定, 其接受一个匿名函数,并调用它,调用匿名函数时传入一个新建的 channel,一般匿名函数会操作这个 channel,最后会将这个 channel 返回。
chnl = Channel(c->foreach(i->put!(c,i), 1:4));
这里的foreach接收一个匿名函数和一个可迭代的对象,foreach 将对象的每一个迭代值都应用到匿名函数上。
抽象类型在 julia 的类型系统中起到构建类型树(type graph),复用逻辑和实现多态的作用。类型树的根类型是Any, 任意类型都是它的子类型(subtype), 叶子类型是Union{}, 和Any相反,任意类型都是Union{}的父类型。我们来看下,julia 的数值类型部分的类型树:
abstract type Number end
abstract type Real <: Number end
abstract type AbstractFloat <: Real end
abstract type Integer <: Real end
abstract type Signed <: Integer end
abstract type Unsigned <: Integer end
数值类型的根是Number, 之后由它逐步构建出所有的数值类型。
tip: A <: B为真则 A 是 B 的子类型成立
julia> if Int64 <: Number
println("hello")
end
hello
struct 的定义, 初始化及访问都是标准的方式:
julia> struct Foo
bar
baz::Int
qux::Float64
end
julia> foo = Foo("Hello, world.", 23, 1.5)
Foo("Hello, world.", 23, 1.5)
julia> foo.bar
"Hello, world."
不指定类型的字段,默认类型为Any。特殊的地方是,struct 默认是不能修改的:
julia> foo.bar = 1
ERROR: type Foo is immutable
只能通过它的构造器重新初始化。要使其可修改需要显式地声明mutable, mutable struct 会分配在堆内存上。
定义和初始化都比较常规
julia> IntOrString = Union{Int,AbstractString}
Union{AbstractString, Int64}
julia> 1 :: IntOrString
1
julia> "Hello!" :: IntOrString
"Hello!"
这里只说下 julia 的值传递规则,对于不可修改的对象,在赋值或者作为入参时是值传递(copy), 可修改的对象是通过指针传递(sharing via pointers), 特别的,不可修改的大内存对象也是指针传递。[4]
Nullable
function calc() ::Nullable{Int64}
# return 1
# no return
# return Nullable(1)
end
v = calc()
if !isnull(v)
println(get(v))
end
可以将函数用 Task 包裹起来,通过 Task 的接口,控制任务的执行。
julia> a1() = det(rand(1000, 1000));
julia> b = @task a1();
julia> istaskstarted(b)
false
julia> schedule(b);
julia> yield();
julia> istaskdone(b)
true
julia 的变量比较特殊的地方是,它可以用 Unicode(UTF-8)作为名字, 因为科学计算中有很多特殊的数学符号。
julia> δ = 0.00001
1.0e-5
julia> 안녕하세요 = "Hello"
"Hello"
有一个问题是,这些特殊符号怎么输入?在 julia 的 repl 中,可以用\加单词打印出特殊字符,比如上述的δ符号,英文名叫 delta, 在 repl 里输入:
julia> \delta
然后按 tab 键,即可打印出δ。
为了科学计算的便利,julia 内置了很多常量和函数, 比如pi, sqrt等,且可以修改它们。
julia> pi
π = 3.1415926535897...
julia> pi = 3
WARNING: imported binding for pi overwritten in module Main
3
julia> pi
3
julia> sqrt(100)
10.0
julia> sqrt = 4
WARNING: imported binding for sqrt overwritten in module Main
4
另外,变量的定义称为变量绑定,变量没有类型,值有类型,变量名和值是绑定关系。我们可以从类型的声明上来窥探出这一点, 在 C 里面给变量声明一个类型并初始化可以这样写:
// c
float a = 8;
在 Julia 里这样写:
a = 8 ::Float32
唉?不对,repl 报错了
julia> a = 1 ::Float32
ERROR: TypeError: typeassert: expected Float32, got Int64
编译器认为 1 是 Int64, 而我们尝试给它指定一个 Float32 的类型,所以报错了,说明 1 这个值已经有了自己的类型,赋值操作仅仅是将变量名和值进行绑定。
tip: 全局变量不能声明类型。
| Expression | Name | Description |
|---|---|---|
+x |
unary plus | +(1,2,3)=6 |
-x |
unary minus | 如果-x = y , 则必然 y + x = 0, 用来表示负数的 |
x + y |
binary plus | performs addition |
x - y |
binary minus | performs subtraction |
x * y |
times | performs multiplication |
x / y |
divide | performs division |
x \ y |
inverse divide | equivalent to y / x |
x ^ y |
power | raises x to the yth power |
x % y |
remainder | equivalent to rem(x,y) |
| !x | negation | changes true to false and vice versa |
~x |
bitwise not | |
x & y |
bitwise and | |
x | y |
bitwise or | |
x ⊻ y |
bitwise xor (exclusive or) | |
x >>> y |
logical shift right | 整体向右移动,并在左边补 0 |
x >> y |
arithmetic shift right | 整体向右移动,并在最高位填充符号位 |
x << y |
logical/arithmetic shift left | 整体向左移动,并在右边补 0 |
| += -= *= /= = ÷= %= ^= &= |= ⊻= >>>= >>= <<= | 运算并赋值的简写形式 | |
| . | dot operator | 可以和二元操作符比如 ^, %结合,用来对数组进行运算, ex. [1,2].^2 的结果为[1, 4] |
== |
equality | |
!=, ≠ |
inequality | |
< |
less than | |
<=, ≤ |
less than or equal to | |
> |
greater than | |
>=, ≥ |
greater than or equal to | |
| === | 对象判等 | 对于可修改的对象,用内存地址来判等,对于不可修改的对象,通过对象的二进制数据来判等 |
| ?: | 条件运算符 |
大部分语言中使用花括号{}来包裹相关联的表达式:
{
let x = 1;
let y = 2;
let z = x + y;
}
而 julia 使用 begin..end 来包裹
begin
x = 1
y = 2
println(x+y)
end
if x < y
println("x is less than y")
elseif x > y
println("x is greater than y")
else
println("x is equal to y")
end
和拥有隐式类型转换的语言不同,这种写法会报类型错误
julia> if 1
return 2;
end
ERROR: TypeError: non-boolean (Int64) used in boolean context
while 语句。此类通用语法,不再一一列举。
while true
println("OK!")
break
end
for i = 1:1000
for i in [1,4,0]
for s ∈ ["foo","bar","baz"]
try
throw(DomainError("foo"))
catch e
println(e)
end
上述代码可以合并成一行, 为了避免 catch 后的变量和之后的表达式混淆,用;来分割它们。
try throw(BoundsError("bar")) catch e; println(e) end
当你不需要处理错误的时候,可以省略 catch
try throw(BoundsError("bar")) end
和 Java 一样,配合 try..catch 使用
f = open("file")
try
# operate on file f
finally
close(f)
end
begin..end 包裹起来的多个表达式可以当作一个表达式来求值
v = begin
x = 1
y = 2
x + y
end
println(v)
还有另外两种同样作用的写法:
v = (x=1; y=2; x+y)
println(v)
v = begin x = 1; y = 2; x + y end
println(v)
中文名为短路求值,是一种基于逻辑运算符的求值方法, 有点类似于条件表达式
true || 1
上述表达式的值为 1,因为左边的表达式为真值,右边的表达式会被求值并返回/赋值
false && 2
上述表达式的值为 false,因为左边的值为假值,因此右边的表达式会被忽略。我们来看一个使用此写法的阶乘函数:
function fact(n::Int)
n >= 0 || error("n must be non-negative")
n == 0 && return 1
n * fact(n-1)
end
println(fact(5))
Julia 使用const定义常量,将 global 里的常量用 const 标记,有助于 JIT 优化执行速度,局部作用域里的常量可以不用 const 标记,编译器能够自动将其识别出来。
Julia 的作用域不算特殊,主要有 GLobal,Local,Module 这三种作用域。
每个 module 都有独立的 Global Scope,module 之间需要先引用才能访问, 但是 module A 的变量在 module B 里是只读的
语句都会产生一个 local scope, 除了begin..end, if语句。总的来说,local scope 的所有父级作用域里的变量在 local scope 是可见的,反之则不可见,这和我们的经验是一致的。
如果需要让 local scope 里的变量在父级作用域里可见,可以强制定义为 global 变量
for i = 1:3
global x=i
end
x # 3
如果 local scope 和 global scope 都有变量 x,同名了,怎么办?
如果不想用 global 里的 x,可以将 local 里的变量 x 标记为 local, 或者在 local scope 里对 x 重新赋值
// case1
x,y=0,1
function plus()
x=1 # or local x = 1
return x+y
end
plus() # 2
x # 0
y # 1
上述代码 x 被重新赋值,新产生了一个局部变量 x,和 global 里的 x 不冲突。
如果想用 global 里的 x 呢?按照总规则,global 的 x 在 local scope 里是天然可见的,直接使用即可。
// case2
x,y=0,1
function plus()
return x+y
end
plus() # 1
x # 0
y # 1
如果不仅仅是使用,还要修改 global x 呢(当然这么做是不推荐的)?在 case1 当中,x 被修改后,就自动变成 local 的变量了,因此要将 x 指明为 global 再修改,如下:
// case3
x,y=0,1
function plus()
global x=100
return x+y
end
plus() # 101
x # 100
y # 1
你们有没有发现 case1 和 case3 本质上是一样的?都是用关键字显式地指明它所在的作用域。
模块的引入主要是为了引入新的作用域和组织代码结构。定义一个 module 的方式:
module MyModule
export fn # 需要暴露的的变量或方法使用 export 来标记
fn() = "x"
end
导入的方式有两种,using和import,它们的区别在于引入的内容的使用方式,import 会将引入的模块的名称暴露在当前空间,然后通过模块名来使用引入的内容
import MyModule
MyModule.fn()
using 会将模块导出的所有内容直接暴露在当前空间,使用时不需要模块名
using MyModule
fn()
在 Java 里,我们对一个 Integer 数组使用函数式的方法来操作可以这么写:
array.stream()
.filter(x -> x %2 == 0)
.map(x -> x*x)
.collect(Collectors.toList())
Julia 提供了类似的操作方式:
array = [1,3,4,5,7,10]
array = filter(x -> x % 2 == 0, array)
array = map(x -> x^2, array)
println(array) # [16, 100]
除了 filter, map 之外,julia 还提供了 reduce, mapreduce 等函数
array = mapreduce(x->x+10, +, array) # (16+10) + (100+10)
println(array) # 136
在 subtype 的章节中,我们介绍了 julia 的类型树,自然 Julia 提供了扩充类型的方式,即抽象类型,定义一个抽象类型:
abstract type Graph end
它的默认父类是Any, 我们在定义的时候也可以指定父类
abstract type Graph <: Any end
和 Rust,golang 等语言不同的是,我们并不能为一个 struct 类型定义函数,所以我们看到的仍然是多重派发,而不是其他语言的惯用写法,在理解的时候要暂时抛弃已有的 OOP 概念,不管是 Go,Rust 还是 Julia,传统的 OOP 都被摒弃了。
struct Circle <: Graph
radius ::Float64
x ::Int64
y ::Int64
end
struct Rec <: Graph
width ::Float64
height ::Float64
x ::Int64
y ::Int64
end
function area(r ::Circle) ::Float64
return pi * r.radius^2
end
function area(g ::Rec)
return g.x*g.y
end
println(area(Circle(1.0, 1, 1)))
println(area(Rec(1.0, 1.0, 2, 2)))
可能你会觉得上面的代码并不 OOP,我也这么认为,这里举另外一个例子:
abstract type AbstractGraph <: Any end
struct Graph{T}
x ::Integer
y ::Integer
v ::T
end
struct Circle <: AbstractGraph
radius ::Float64
end
struct Rec <: AbstractGraph
width ::Float64
height ::Float64
end
showLoc(g ::Graph{<:AbstractGraph}) = println("(", g.x, ",",g.y ,")")
area(g ::Graph{Circle}) = println(pi * g.v.radius^2)
area(g ::Graph{Rec}) = println(g.v.width * g.v.height)
showLoc(Graph{Circle}(1,1, Circle(1.0)))
showLoc(Graph{Rec}(1,1, Rec(1,2)))
area(Graph{Circle}(1,1, Circle(1.0)))
area(Graph{Rec}(1,1, Rec(1,2)))
不知道这么写是否让你觉得更 OOP 一点?
julia 的宏和 C/C++一样,使用的是文本替代的方式。一个宏将一组参数映射成一个 return 语句,类似于函数的定义。定义一个宏:
macro say()
return "Hi"
end
println(@say) # 调用时使用@加宏名
我们知道,代码里是有表达式的,它们在运行时被编译器求值,同样地我们可以自己创建一个表达式对象,手动来求值。
a = 1
b = 1
ex = :($a+$b)
println(eval(ex))
julia 可以使用反引号包裹一段 shell, Perl 或 Ruby 代码, 并执行这段代码
julia> file = "/etc/passwd"
"/etc/passwd"
julia> readstring(`sort $file`)
“#\n# \n# Note that this file is consulted directly only when the system
...
julia 是一门为科学计算而生的语言,在科学计算里多维数组是一种很常见的数据表达方式。
除了常规的初始化方式之外, julia 提供了更高级的数组构建方式:
fn(x) = x^2
[fn(x) for x=1:10]
当然,可以直接将函数写在表达式内:
[x^2 for x=1:10]
这种方式叫推导(comprehensions), 上面的代码会生成一个一维数组
[1, 4, 9, 16, 25, 36, 49, 64, 81, 100]
以此类推,可以生成一个多维数组:
[x+y for x=1:10, y=1:10]
当 x,y 的值有联系时:
[(i,j) for i=1:3 for j=1:i]
julia 提供了很多多维数组的操作函数,比如 reshape 函数,将 n*m 的数组转换成 x*y 的数组,且 n*m=x*y.
reshape([x+y for x=0:1, y=1:10], (4,5))
上述代码,将 2*10 的数组转换成 4*5 的数组。其他的操作函数可以查看文档。
julia 内置了很多线性代数的算法,比如计算一个 n*n 矩阵的迹数
julia> A = [1 2 3; 4 1 6; 7 8 1]
3×3 Array{Int64,2}:
1 2 3
4 1 6
7 8 1
julia> trace(A)
3
这里不再一一列举,感兴趣的可以查看文档.