作者: songtianyi 2018-09-25
这两天在看防火墙策略相关的论文,多篇论文中都反复提到了二元决策图(binary decision diagram,BDD),一种用于表示防火墙策略的数据结构, 也称为二元判定图。二叉决策树我们听的多了,二元决策图我还是第一回看到,写篇文章记录一下。为了方便叙述,下文中的二元决策图均用 BDD 来代替。
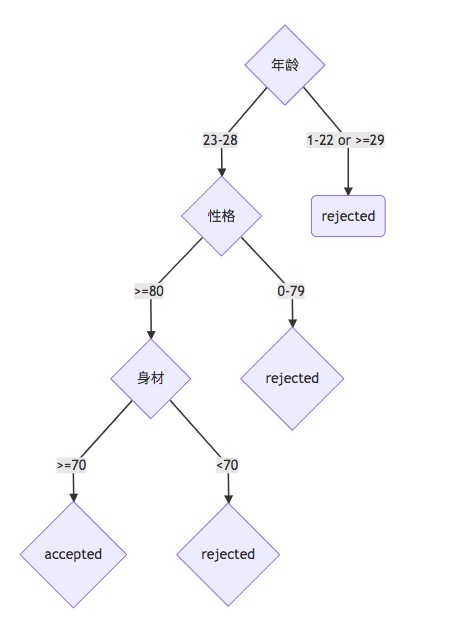
在学习 BDD 之前,我们先回顾一下二叉决策树(BDT)的内容,我想它们之间一定有一些共性。二叉决策树的主要应用是分类,通过度量一系列的属性,将输入分成两类甚至多类。用一个通俗的择偶过程来举例一个简单的二叉决策树的构造:

在上图中,我们通过年龄,性格和身材将择偶对象简单分成了两类,接受和拒绝。年龄,性格和身材我们都将其看成是离散的整形值,然后划分成两个集合,比如把年龄分成[23, 28], [1, 22] ∪ [29, +∞),决策结果分别对应于接受和拒绝,决策的过程由决策函数来完成, 比如对于年龄的决策:
func f(age int) bool {
return age >= 23 && age <= 28
}
以此类推,遍历整棵树完成所有决策过程。看到这里大家应该会有这样的疑问: 为什么先判断的是年龄,而不是性格或者身材呢? 这个决策顺序的确是很有讲究的,顺序不同,整个决策过程所需的计算次数也不同,从经验上讲,年龄的判断是最简单的,假设输入的择偶对象是随机抽样出来的,按照现在的人口年龄比例,属于[23, 28]集合的对象远比属于[1, 22] ∪ [29, +∞)集合的少,这样通过年龄可以过滤掉大部分对象。但实际的案例并不会像这个例子这么简单,单凭经验是无法构造出一个复杂度较低的决策树的。
即第三代迭代二叉树算法,是一种二叉树构造算法,用于解决如何构造最优二叉决策树的问题。这里不详细讲它,简单来说,它会计算出各个属性的增益率,先根据增益率最大的属性做决策,可以理解为它是一种剪枝算法。
C4.5 是对 ID3 的改进。
BDD 是用来表达布尔函数的数据结构,它的初始形态也是二叉决策树,从上一小节的二叉决策树的示例图和决策过程不难看出来它的运算方式是:
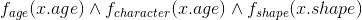
x 为择偶对象,x = {age, character, shape}, 我们将其换成一般性的布尔函数, 表示为:
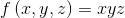
那么对于布尔函数(电路中的与-或门):
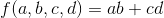
它的二叉决策树构造为:
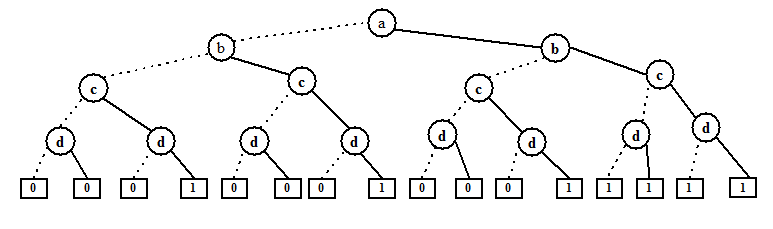
虚线表示变量被赋值为 0,其连接的末端节点称为 low child,实线表示变量被赋值为 1,其连接的末端节点称为 high child. 叶子节点(0|1)称为 terminal node, 非 terminal node 称为 decision node. 可以看到,terminal node 的数量为 24, 随着变量数的上升,BDT 的结果空间会指数级增加,它的局限性就体现出来了。结果空间很大,但结果集只有[0, 1], 说明存在优化的空间,这里直接给出优化的规则:
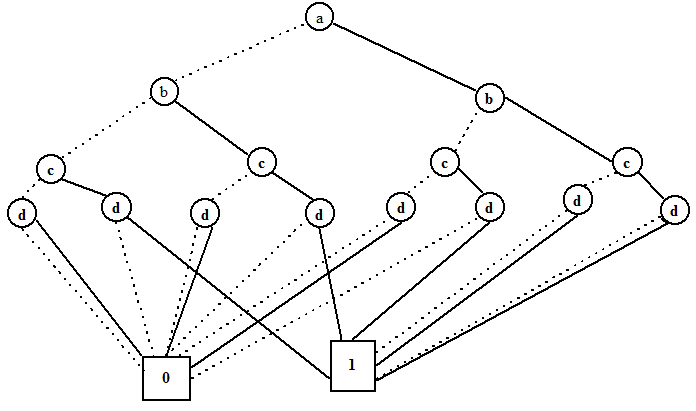
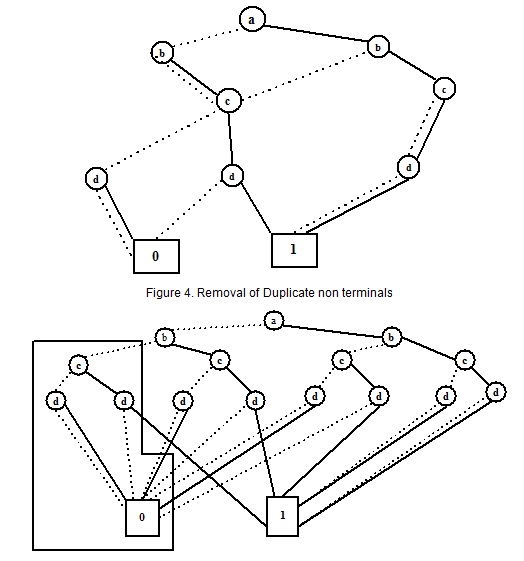
经过这三个无损(不影响结果)的消除规则优化的 BDD 称为 RBDD(Reduced Binary Decision Diagram), 它是一个有向无环图(DAG). 我们以图的形式讲述了从布尔函数到 BDT 再到 BDD 的过程,但是代码却不能这么写,前边提到了 BDT 会占用较大的空间,通用的做法是利用香农展开(也叫香农分解)来构造布尔函数的 RBDD.
香农展开(英语:Shannon's expansion),或称香农分解(Shannon decomposition)是对布尔函数的一种变换方式。它可以将任意布尔函数表达为其中任何一个变量乘以一个子函数,加上这个变量的反变量乘以另一个子函数。3例如对于布尔函数:
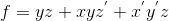
我们选取 x 变量及其反变量作为被乘数, 那么最终的结果可以先记为:
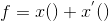
根据分解前的内容我们能够推算出部分括号里的内容:
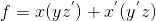
但少了一项 yz , 在布尔代数中有:
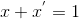
所以最终的分解的结果为:
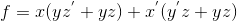
更一般地,对于布尔函数 f , 选取变量 x 及其反变量作为被乘数,它的香农分解结果为:
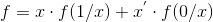
其中, f(1/x) 表示,将 f 中的 x 用 1 代替, f(0/x) 表示,将 f 中的 x 用 0 代替。按照这种方法,对于之前的决策图的布尔函数的例子,一个完整的香农分解和还原过程如下:
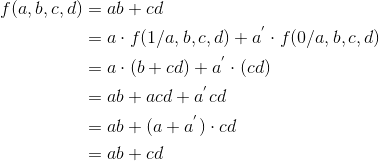
那么我们如何基于香农分解来构造 RBDD 呢?依次选取 a, b 作为被乘数,可以得到:
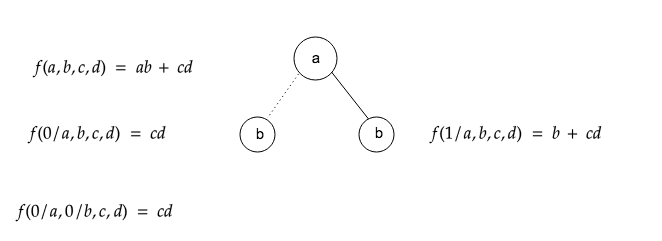
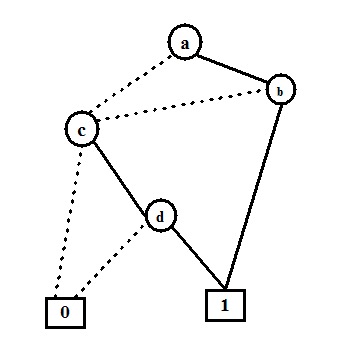
可以看出,当 a 被赋值为 0,b 无论被赋值为 0 还是 1,其结果都是 cd , 因此当 a 被赋值为 0 的时候,b 节点可以消除, 依次类推得到完整的 RBDD 图:
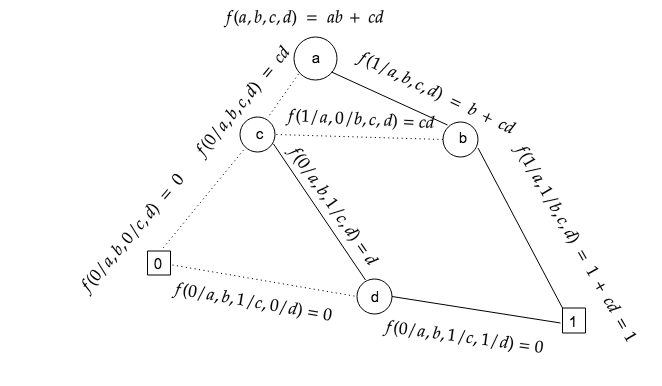
即 Reduced ordered binary decision diagram. 我们在用香农分解构造 RBDD 的时候,变量的选取顺序是 a, b, c, d, 我们知道,在构造二叉决策树的时候,变量的顺序对于整个过程的复杂度影响很大,同样的,不同的变量顺序也会构造出不同的 RBDD 图,节点数也会有差异,那么就存在一个最佳变量顺序,依照最佳顺序可以构建出最小的 RBDD 图。但是,找到这个最佳顺序是一个 NP 难(NP-hard)问题。